梅森素数（素数计算方法）

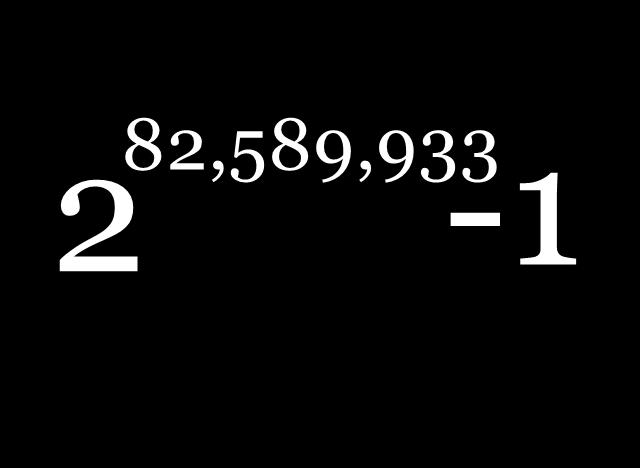
梅森素数

素数计算方法

梅森素数，它是发现已知最大素数的有效途径，它推动了数论研究，也促进了计算数学、程序设计技术、网格计算技术以及密码技术的发展，梅森素数探究难度较大，它不仅需要高深的理论和纯熟的技巧，而且还需要进行艰巨的计算。

概述

梅森素数，(Mersenne Primes)，17世纪法国数学家、法兰西科学院奠基人马林•梅森，梅森素数指形如2^p－1的正整数，其中指数p是素数，常记为Mp。若Mp是素数，则称为梅森素数。p=2，3，5，7时，Mp都是素数，但M11=2047=23×89不是素数，是否有无穷多个梅森素数是数论中未解决的难题之一。截止2012年7月累计发现47个梅森素数，最大的是p=43,112,609，此时Mp是一个12,978,189位数。

这种素数历来是数论研究的一项重要内容，也是当今科学探索的热点和难点之一，由于梅森素数珍奇而迷人，它被人们誉为“数论中的钻石”。

历史发现

早在公元前300多年，古希腊数学家欧几里得就开创了研究2^P－1的先河，他在名著《几何原本》第九章中论述完美数时指出：如果2^P－1是素数，则2^P－1（2^P－1）是完美数。

1640年6月，费马在给梅森的一封信中写道：“在艰深的数论研究中，我发现了三个非常重要的性质。我相信它们将成为今后解决素数问题的基础”，这封信讨论了形如2^P－1的数（其中p为素数）。梅森在欧几里得、费马等人的有关研究的基础上对2^P－1作了大量的计算、验证工作。

1644年，在他的《物理数学随感》一书中断言：对于p=2，3，5，7，13，17，19，31，67，127，257时，2^P－1是素数；而对于其他所有小于257的数时，2^P－1是合数。前面的7个数（即2，3，5，7，13，17和19）属于被证实的部分，是他整理前人的工作得到的；而后面的4个数（即31，67，127和257）属于被猜测的部分。

1772年，瑞士数学家欧拉在双目失明的情况下，靠心算证明了M31是一个素数，它共有10位数，堪称当时世界上已知的最大素数，他因此获得了“数学英雄”的美誉。这是寻找已知最大素数的先声。欧拉还证明了欧几里得关于完美数的定理的逆定理，即：每个偶完美数都具有形式2^P－1（2^P－1），其中2^P－1是素数。这就使得偶完美数完全成了梅森素数的“副产品”了。

1883年，数学家波佛辛利用鲁卡斯定理证明了M61也是素数——这是梅森漏掉的。梅森还漏掉另外两个素数：M89和M107，它们分别在1911年与1914年被数学家鲍尔斯发现。

1903年，在美国数学学会的大会上，数学家柯尔作了一个一言不发的报告，他在黑板上先算出2^67－1，接着又算出193707721×761838257287，两个结果相同，这在美国数学学会开会的历史上是绝无仅有的一次。他第一个否定了“M67为素数”这一自梅森断言以来一直被人们相信的结论。1922年，数学家克莱契克进一步验证了M257并不是素数，而是合数（但他没有给出这一合数的因子，直到20世纪80年代人们才知道它有3个素因子）。

1930年，美国数学家雷默改进了鲁卡斯的工作，给出了一个针对Mp的新的素性测试方法，即鲁卡斯-雷默方法：Mp＞3是素数的充分必要条件是Lp-2=0，其中L0=4，Ln+1=(Ln－2)ModMp。这一方法直到今天的“计算机时代”仍发挥重要作用。

1952年，数学家鲁滨逊等人将鲁卡斯-雷默方法编译成计算机程序，使用SWAC型计算机在短短几小时之内，就找到了5个梅森素数：M521、M607、M1279、M2203和M2281。其后，M3217在1957年被黎塞尔证明是素数；M4253和M4423在1961年被赫维兹证明是素数。

1963年，美国数学家吉里斯证明M9689和M9941是素数。1963年9月6日晚上8点，当第23个梅森素数M11213通过大型计算机被找到时，美国广播公司（ABC）中断了正常的节目播放，以第一时间发布了这一重要消息；发现这一素数的美国伊利诺伊大学数学系全体师生感到无比骄傲，以致于把所有从系里发出的信件都敲上了“2^11213－1是个素数”的邮戳。

1971年3月4日晚，美国哥伦比亚广播公司（CBS）中断了正常节目播放，发布了塔可曼使用IBM360-91型计算机找到新的梅森素数M19937的消息。而到1978年10月，世界几乎所有的大新闻机构（包括中国的新华社）都报道了以下消息：两名年仅18岁的美国高中生诺尔和尼科尔使用CYBER174型计算机找到了第25个梅森素数：M21701。

1979年2月23日，当美国克雷研究公司的计算机专家史洛温斯基和纳尔逊宣布他们找到第26个梅森素数M23209时，人们告诉他们：在两个星期前诺尔已得到这一结果。为此，史洛温斯基潜心发愤，花了一个半月的时间，使用CRAY-1型计算机找到了新的梅森素数M44497。

1983年至1985年间找到了3个梅森素数：M86243、M132049和M216091。但他未能确定M86243和M216091之间是否有异于M132049的梅森素数。

1988年，科尔魁特和韦尔什使用NEC-FX2型超高速并行计算机果然捕捉到了一条“漏网之鱼”——M110503。

1992年3月25日，英国原子能技术权威机构——哈威尔实验室的一个研究小组宣布他们找到了新的梅森素数M756839。

1994年1月14日，史洛温斯基和盖奇为其公司再次夺回发现“已知最大素数”的桂冠——这一素数是M859433。

在1996年，梅森素数M1257787仍是他们的成果，这一素数是使用CRAY-794超级计算机取得的，史洛温斯基由于发现7个梅森素数，而被人们誉为“素数大王”。

2004年5月15日，美国国家海洋和大气局顾问、数学爱好者乔希·芬德利(Josh Findley)用一台装有2.4GHZ奔腾处理器的个人计算机，找到了当时世界上已知最大的梅森素数。该素数为2的24036583次方减1(即2^24036583－1)，它有7235733位数，如果用普通字号将这个数字连续写下来，它的长度可达3万米，它是2000多年来人类发现的第41个梅森素数，也是当时已知的最大素数。

2005年2月28日，一名德国数学爱好者于2月18日发现了一个新的素数，这个素数有7816230位，可以写成2^25964951-1。

2007年秋季，美国加州大学洛杉矶分校(UCLA)的计算机专家埃德森·史密斯利用数学系所有的计算机参加了一个名为“因特网梅森素数大搜索”(GIMPS)的国际合作项目，前不久他在其中的一台计算机上偶然发现了这个超大的素数。这是人类迄今为止发现的第46个也是最大的梅森素数。2^43112609-1，也就是2自身相乘43112609次减1，它有12978189位数，如果用普通字号将这个巨数连续写下来，这个梅森素数的长度可超过50公里。

分布规律

人们在寻找梅森素数的同时，对其重要性质——分布规律的研究也在进行着。从已发现的梅森素数来看，它们在正整数中的分布时疏时密、极不规则；从发现梅森素数的时间来看，有时许多年未能找到一个，而有时则一下找到好几个。梅森素数已发现的数量很少，且人们对其无穷性尚未可知，因此探索它的分布规律似乎比寻找新的梅森素数更为困难。数学家们在长期的摸索中，提出了一些猜想，英国数学家香克斯、美国数学家吉里斯、法国数学家托洛塔和德国数学家伯利哈特曾分别给出过关于梅森素数分布的猜测。但他们的猜测有一个共同点，就是都以近似表达式给出，而它们与实际情况的接近程度均未尽如人意。

中国数学家和语言学家周海中根据已知的梅森素数及其排列，巧妙地运用联系观察法和不完全归纳法，于1992年2月正式提出了一个关于梅森素数分布的猜想，并首次给出其分布的精确表达式。后来这一重要猜想被国际数学界命名为“周氏猜测”。其内容为：

当2^（2^n）＜p＜2^（2^（n+1））时，Mp有2^（n+1）－1个是素数。

周海中还据此作出了p＜2^（2^（n+1））时梅森素数的个数为2^（n+2）－n－2的推论。（注：n为自然数，p为素数，Mp为梅森数）

周氏猜测自提出以来一直受到人们关注和研究，而且在一些国内外出版的数学辞典和教科书中都有介绍。美籍挪威数论大师、菲尔茨奖和沃尔夫奖得主阿特勒·塞尔伯格认为：周氏猜测具有创新性，开创了富于启发性的新方法；其创新性还表现在揭示新的规律上。

周氏猜测的表达式虽然简单，但破解这一猜测的难度却很大。就目前研究文献来看，一些数学家和数学爱好者尝试破解周氏猜测，却至今未能证明或反证。

研究意义

自古希腊时代直至17世纪，人们寻找梅森素数的意义似乎只是为了寻找完美数。但自梅森提出其著名断言以来，特别是欧拉证明了欧几里得关于完美数的定理的逆定理以来，完美数已仅仅是梅森素数的一种“副产品”了。

寻找梅森素数是发现已知最大素数的最有效的途径，自欧拉证明M31为当时最大的素数以来，在发现已知最大素数的世界性竞赛中，梅森素数几乎囊括了全部。

梅森素数的探究在当代已有了十分丰富的意义。寻找梅森素数是发现已知最大素数的最有效的途径，近百年来找到的“最大素数”几乎都是梅森素数。梅森素数的探究还推动了“数学皇后”——数论的研究，促进了计算技术、密码技术和程序设计技术的发展。

寻找梅森素数是测试计算机运算速度及其他功能的有力手段。如M1257787就是1996年9月美国克雷公司在测试其最新超级计算机的运算速度时得到的。梅森素数在推动计算机功能改进方面发挥了独特作用。发现梅森素数不仅仅需要高功能的计算机，它还需要素数判别和数值计算的理论与方法以及高超巧妙的程序设计技术等等，因而它还推动了数学皇后——数论的发展，促进了计算数学、程序设计技术的发展。

梅森素数在实用领域也有用武之地，现在人们已将大素数用于现代密码设计领域。其原理是：将一个很大的数分解成若干素数的乘积非常困难，但将几个素数相乘却相对容易得多。在这种密码设计中，需要使用较大的素数，素数越大，密码被破译的可能性就越小。

寻找梅森素数促进了分布式计算技术的发展。从最新的7个梅森素数是在因特网项目中发现这一事实，分布式计算技术使得用大量个人计算机去做本来要用超级计算机才能完成的项目成为可能；这是一个前景非常广阔的领域。

梅森素数促进了当代计算技术、密码技术、程序设计技术的发展以及快速傅立叶变换的应用。梅森素数的意义还在于它促进了网格技术的发展；而网格技术是一项应用非常广阔的高新技术。另外，梅森素数还可用来测试计算机硬件运算是否正确。[1]

相关命题和定理

性质

q≡3mod4为素数。则2q+1是素数的充分必要条件是2q+1整除Mq。

拉马努金给出：方程Mq=6+x2当q为3、5和7时有三个解；q为合数时有2个解。

如果p是奇素数，那么任何能整除2p−1的素数q都一定是1加上一个2p的倍数。例如，211−1=23×89，而23=1+2×11，89=1+8×11。

如果p是奇素数，那么任何能整除的素数q都一定与同余。

计算公式

由计算公式知：q是素数是Mq是素数的必要条件。但这不是充分的。M11=211−1=23×89是个反例。

对Mq（q是素数）有：

若a是Mq的因数，则a有如下性质：

a≡1mod2qa≡±1mod8

欧拉的一个关于形如1+6k的数的理论表明：Mq是素数当且仅当存在数对（x,y）使得Mq=(2x)2+3(3y)2，其中q≥5。

最近，Bas jansen研究了等式Mq=x2+dy2（0≤d≤48），得出了一个对于d=3情况下的新的证明方法。

Reix发现q>3时，Mq可以写成：Mq=(8x)2(3qy)2=(1+Sq)2-(Dq)2。显然，若存在一个数对（x,y），那么Mq是素数。

素数检验

卢卡斯-莱默检验法是现在已知的检测梅森数素数的最好的方法。该方法由爱德华·卢卡斯于1878年发现，并由莱默1930年代作了改进，因此得名。该方法基于循环数列的计算，其原理是：

Mn为素数当且仅当Mn整除Sn-2（S0=4，Sk=Sk−12−2，k>0）。

与完全数的关系

梅森素数与偶完全数有一一对应的关系。前4世纪，欧几里得（Euclid）证明如果M是梅森素数，那么M(M+1)/2是完全数。18世纪，欧拉（Euler）证明所有的偶完全数都有这种形式。

相关问题和猜想

梅森素数是否有无穷多个？这是尚未解决的著名数学谜题；而揭开这一未解之谜，正是科学追求的目标。

参考资料

1.梅森素数是什么·钱来也