正弦定理(数学定理)
温馨提示:这篇文章已超过393天没有更新,请注意相关的内容是否还可用!

正弦定理
数学定理
正弦定理(The Law of Sines)是三角学中的一个基本定理,它指出“在任意一个平面三角形中,各边和它所对角的正弦值的比相等且等于外接圆的直径”,即(为外接圆半径,为直径)。正弦定理是解三角形的重要工具。正弦定理指出了任意三角形中三条边与对应角的正弦值之间的一个关系式。一般地,把三角形的三个角和它们的对边叫做三角形的元素。一般地,已知两边和其中一边的对角解三角形,有两解、一解、无解三种情况,可参考三角形性质、钝角三角形性质进行判断。
| 中文名 | 正弦定理 |
| 外文名 | The Law of Sines |
| 提出者 | 纳绥尔丁 |
| 应用学科 | 数学 |
| 适用领域范围 | 三角函数 |
| 提出时间 | 公元10世纪 |
| 突出贡献者 | 韦达、海伦、秦九韶 |
发展简史
历史上,正弦定理的几何推导方法丰富多彩。根据其思路特征,主要可以分为两种。
第一种方法可以称为 “同径法 ”,最早为13世纪阿拉伯数学家、天文学家纳绥尔丁和15世纪德国数学家雷格蒙塔努斯所采用。“同径法 ”是将三角形两个内角的正弦看作半径相同的圆中的正弦线(16世纪以前,三角函数被视为线段而非比值),利用相似三角形性质得出两者之比等于角的对边之比。纳绥尔丁同时延长两个内角的对边,构造半径同时大于两边的圆。雷格蒙塔努斯将纳绥尔丁的方法进行简化,只延长两边中的较短边,构造半径等于较长边的圆。17~18世纪,中国数学家、天文学家梅文鼎和英国数学家辛普森各自独立地简化了“同径法”。
18世纪初,“同径法”又演化为“直角三角形法”,这种方法不需要选择并作出圆的半径,只需要作出三角形的高线,利用直角三角形的边角关系,即可得出正弦定理。19世纪,英国数学家伍德豪斯开始统一取R=1,相当于用比值来表示三角函数,得到今天普遍采用的 “作高法”。
第二种方法为“外接圆法”,最早为16世纪法国数学家韦达所采用。韦达没有讨论钝角三角形的情形,后世数学家对此作了补充。
定理定义
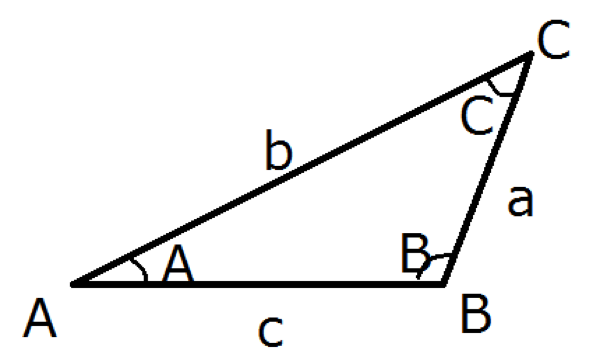
在任意中,角 所对的边长分别为,三角形外接圆的半径为 ,直径为则有
一个三角形中,各边和所对角的正弦之比相等,且该比值等于该三角形外接圆的直径(半径的2倍)长度。
验证推导
 图示1
图示1证明一
做一个边长为 的三角形,对应角分别是 从角向边做垂线,得至 一个长度为的垂线和两个直角三角形。
很明显:
和
因此:
和
同理:
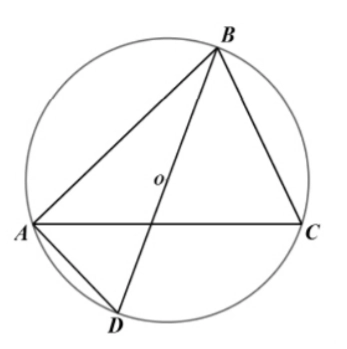
证明二:外接圆
(1)锐角三角形中
如图2,作 的外接圆, 为圆心。连结 并延长交圆于 , 设 。根据直径所对圆周角是直角及同弧所对圆周角相等,可得: 。
同理可证 。
。
(2)直角三角形中
因为 ,可以得到
所以可以证明
(3)正角三角形中
线段是圆的直径 根据圆内接四边形对角互补的性质 所以
因为为外接圆的直径 根据正弦定义
变形可得
根据以上的证明方法可以证明得到得到三角形的一条边与其对角的正弦值的比等于外接圆的直径,即
 图示3
图示3证明三: 向量
若 为锐角三角形,过点作单位向量 , 则与 的夹角为与 的夹角为 . 由向量的加法原则可 得
为了与图中有关角的三角函数建立联系,我们在上面向量等式的两边同取与向量的数量积运算,得到
即
同理,过点作与垂直的单位向量, 则与 的夹角为 与的夹 角为 ,
可得
若为正角三角形,不妨设 过点作与 垂直的单位向量 , 则的夹角为, 与 的夹角为同理
,
即
过点作与垂直的单位向量, 则 与 的夹角为 , 与 的夹角为 , 可得
综上,。
定理意义
正弦定理指出了任意三角形中三条边与对应角的正弦值之间的一个关系式。由正弦函数在区间上的单调性可知,正弦定理非常好地描述了任意三角形中边与角的一种数量关系。
一般地,把三角形的三个角和它们的对边叫做三角形的元素。已知三角形的几个元素求其他元素的过程叫做解三角形。正弦定理是解三角形的重要工具。
定理推广
1、在解三角形中,有以下的应用领域:
已知三角形的两角与一边,解三角形。
已知三角形的两边和其中一边所对的角,解三角形。
运用解决角之间的转换关系。
注意:
解三角形时,已知两角与一边,三角形是确定的,利用正弦定理解三角形时,其解是唯一的;已知三角形的两边和其中一边的对角,由于该三角形具有不稳定性,所以其解不确定,可结合平面几何作图的方法及“大边对大角,大角对大边”定理和三角形内角和定理去考虑解决问题。
一般地,已知两边和其中一边的对角解三角形,有两解、一解、无解三种情况,可参考三角形性质、钝角三角形性质进行判断。若已知的对边与的夹边,则:
对于钝角三角形,
若,则无解;
若,则有一解;
对于锐角三角形,
若
若,则有一解;
若
若,则有一解。
 钝角三角形
钝角三角形2、三角形面积的计算。
参考资料
1.·
2.·