分解(数学名词)
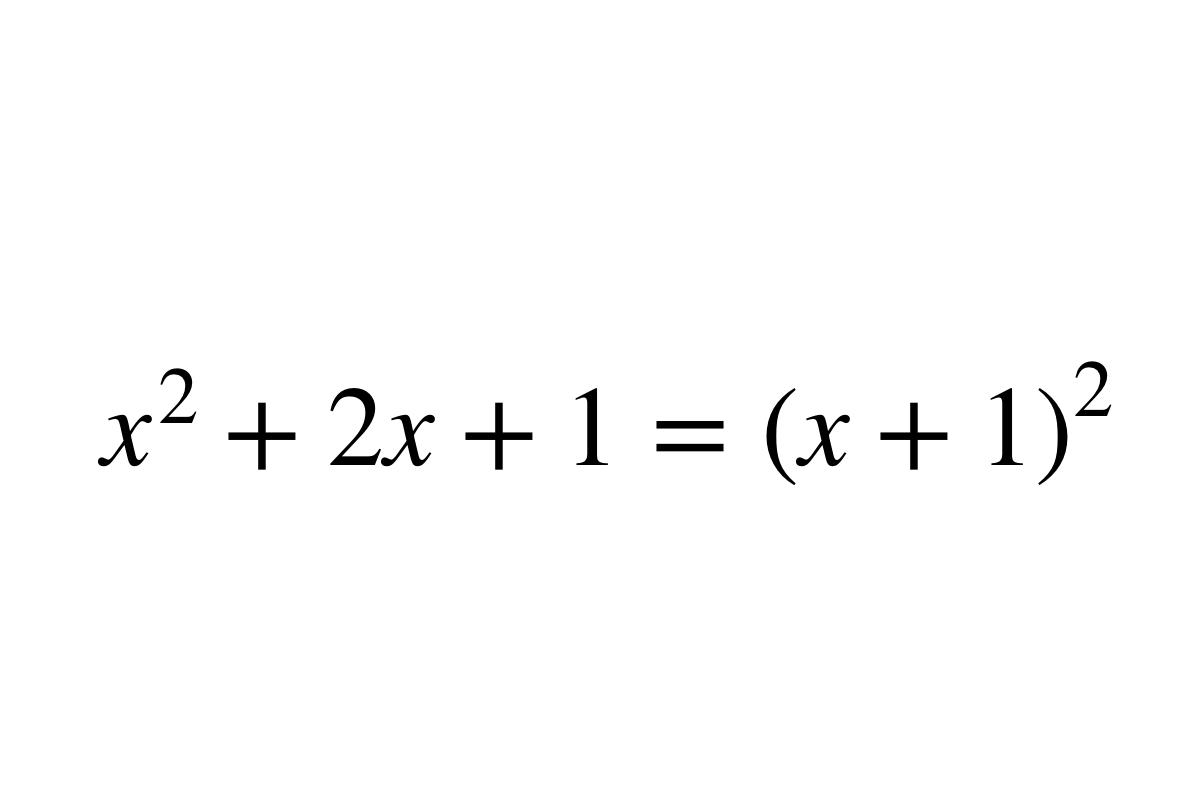
分解
数学名词
分解,数学名词,即和差化积,其最后结果要分解到不能再分为止。初等数学中,把多项式的分解叫因式分解,其一般步骤为:一提二套三分组。要求将多项式分到不可再分的形式。
| 中文名 | 分解 |
| 外文名 | decompose |
| 类型 | 数学名词 |
| 释义 | 和差化积最后要到不能再分解为止 |
| 方法介绍 | 提公因式法、分组分解法等 |
| 公布时间 | 1991年 |
| 见载刊物 | 《化学名词》科学出版社 |
| 定义 | 初等数学中,把多项式的分解叫因式分解,其一般步骤为:一提二套三分组。要求将多项式分到不可再分的形式 |
定义
初等数学中,把多项式的分解叫因式分解,其一般步骤为:一提二套三分组。要求将多项式分到不可再分的形式。
一个多项式要能分解因式,则结果唯一。因为:数域F上的次数大于零的多项式f(x),如果不计零次因式的差异,那么f(x)可以唯一的分解为以下形式:,其中α是f(x)的最高次项的系数,是首1互不相等的不可约多项式,并且Pi(x)(I=1,2…,t)是f(x)的Ki重因式。(*)或叫做多项式f(x)的典型分解式。
分解方法
提公因式法
如果多项式各项都有公共因式,则可先考虑把公因式提出来,即用提公因式法进行因式分解,注意要每项都必须有公因式。
例:
公式法
多项式如果满足特殊公式的结构特征,即可采用套公式法,进行多项式的因式分解,故对于一些常用的公式要求熟悉,除教材的基本公式外,数学竞赛中常出现的一些基本公式现整理归纳如下:
a²-b²=(a+b)(a-b)
a²±2ab+b²=(a±b)²
a³+b³=(a+b)(a²-ab+b²)
a³-b³=(a-b)(a²+ab+b²)
a³±3a²b+3ab²±b²=(a±b)³
a²+b²+c²+2ab+2bc+2ac=(a+b+c)²
a³+b³+c³-3abc=(a+b+c)(a²+b²+c²-ab-ac-bc)
(n为奇数)
说明由因式定理,即对一元多项式f(x),若f(b)=0,则一定含有一次因式x-b。可判断当n为偶数时,当a=b,a=-b时,均有aⁿ-bⁿ=0故aⁿ-bⁿ中一定含有a+b,a-b因式。
注多项式分解时,先构造公式再分解。
分组分解法
当多项式的项数较多时,可将多项式进行合理分组,用分组分解法达到顺利分解的目的。当然可能要综合其他分法,且分组方法也不一定唯一。
十字相乘法
对于形如ax²+bx+c结构特征的二次三项式可以考虑用十字相乘法,
即x²+(b+c)x+bc=(x+b)(x+c)当x²项系数不为1时,同样也可用十字相乘进行操作。
注:“ax⁴+bx²+c”型也可考虑此种方法。
双十字相乘法
在分解二次三项式时,十字相乘法是常用的基本方法,对于比较复杂的多项式,尤其是某些二次六项式,如4x²-4xy-3y²-4x+10y-3,可以运用双十字相乘法分解因式,其具体步骤为:
(1)用十字相乘法分解由前三次组成的二次三项式,得到一个十字相乘图
(2)把常数项分解成两个因式填在第二个十字的右边且使这两个因式在第二个十字中交叉之积的和等于原式中含y的一次项,同时还必须与第一个十字中左端的两个因式交叉之积的和等于原式中含x的一次项。
例:(ab+a)+(b²-b-2)=a(b+1)+(b+1)(b-2)=(b+1)(a+b-2)
拆法、添项法
对于一些多项式,如果不能直接因式分解时,可以将其中的某项拆成二项之差或之和。再应用分组法,公式法等进行分解因式,其中拆项、添项法不是唯一,可解有许多不同途径,对题目一定要具体分析,选择简捷的分解方法。
换元法
换元法就是引入新的字母变量,将原式中的字母变量换掉化简式子。运用此种方法对于某些特殊的多项式因式分解可以起到简化的效果。
待定系数法
待定系数法是解决代数式恒等变形中的重要方法,如果能确定代数式变形后的字母框架,只是字母的系数高不能确定,则可先用未知数表示字母系数,然后根据多项式的恒等性质列出n个含有特殊确定系数的方程(组),解出这个方程(组)求出待定系数。待定系数法应用广泛,在此只研究它的因式分解中的一些应用。
分解因式的方法是多样的,且其方法之间相互联系,一道题很可能要同时运用多种方法才可能完成,故在知晓这些方法之后,要注意各种方法灵活运用。
梅森合数分解
顺带一提,梅森合数分解已经取得一些微不足道的进展:
1、p=4r+3,如果8r+7也是素数,则:(8r+7)|(2^P-1)。即(2p+1)|(2^P-1);
例如:23|(2^11-1);11=4×2+3;
47|(2^23-1);47=4×11+3;
167|(2^83-1);83=4×20+3;
2、p=2^n×3^2+1,则(6p+1)|(2^P-1),
例如:223|(2^37-1);37=2×2×3×3+1;
439|(2^73-1);73=2×2×2×3×3+1;
3463|(2^577-1);577=2×2×2×2×2×2×3×3+1;
3、p=2^n×3^m×5^s-1,则(8p+1)|(2^P-1);
例如:233|(2^29-1);29=2×3×5-1;
1433|(2^179-1);179=2×2×3×3×5-1;
1913|(2^239-1);239=2×2×2×2×3×5-1;
还有一些梅森数分解取得进展,不再一一叙述。
参考资料
1.·